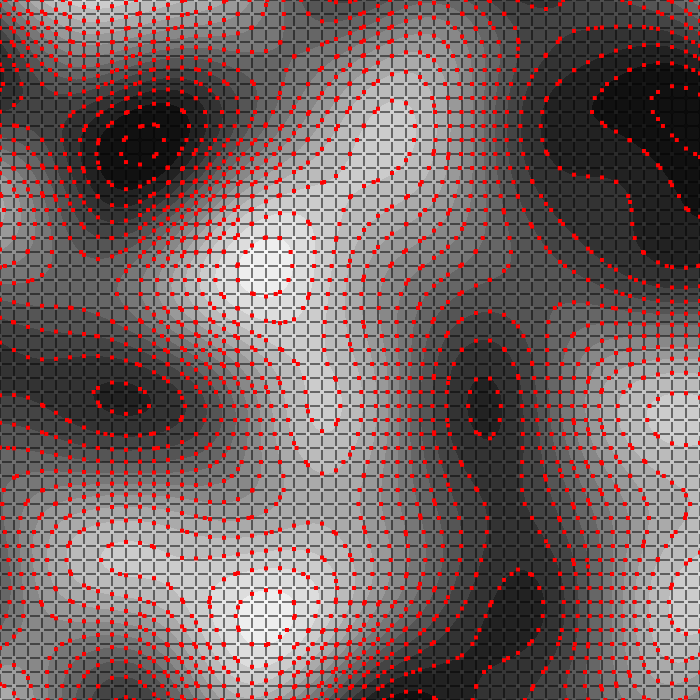
I've always liked the look of contour lines and at one point I wondered how I could extract them from a simplex noise. The underlying reason was that I wanted to extrude them.
Marching squares
The usual solution to achieve that is to use marching squares.
This algorithm divides the plane in squares and uses a lookup table to determine segment configurations.
It is a very interesting algorithm but it can only compute one isovalue at a time. To have all the isolines it has to be applied several times, thus performing some operation multiple times. Also if we want to connect the segments and interpolate their endpoints additionnals steps are required.
Eventually the actual implementation is more tedious than it looks.
A two steps algorithm
The solution I found is also based on a grid. It operates in two steps :
- look at the grid's edges to find interesections with the isolines.
- look at the grid's cells to connect these intersections.
In the marching squares algorithm the points are computed on the edges of the grid. Processing the cells first means that each point is computed twice. Processing the edges first avoids this problem.
However we can't have a lookup table to tell us how to connect the points. Fortunately this is not require and the second part manages to connect the dots.
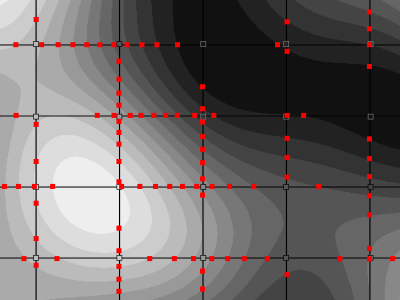

Data structures and initialization
First a few words about the data structures used here. What we want the algorithm to toutput is an array of isolines. An isoline will be represented as a linked-list of what I called PathVertex, which are actually the intersection points computed in the first step.
The Grid is made of Nodes, Edges and Cells. A Nodestores the noise value at a specific location. An Edge stores the intersections between a contour and a segment joining two Nodes. The edge's orientation is givent by the order of the nodes.
A Cell references some Edges with some additional informations. During the second step we'll need to find out whether a path is entering or leaving the cell. This requires us to specify wether the cell lays on the left or the right side of each of its edges and the direction the edges are going to be traversed. When the grid has a specific layout it's possible to keep only one of these two informations and gain a bit of efficiency.
the initialization step is all about building the grid. The algorithm doesn't require the cells to be squares, it could be triangles or irregular polygons... Therefore the grid could be build by placing the nodes at random places and computing a Delaunay triangulation or simply by building a grid of square cells. During this step we can also sample the field where the nodes are located so we won't have to do it everytime we process a segment.
Step 1: Find the intersections between contour lines and the grid's edges
The principle of this step is to retrieve intersections between the contour lines and our grid.
We go through each segment and find wich contour lines it crosses. We don't really compute intersections as we don't have enough information to do so: we only know the values of the field at the end points of the segments.
What we actually do is to simply count how many contour lines the segment must cross.
For example in this configuration we miss some lines:
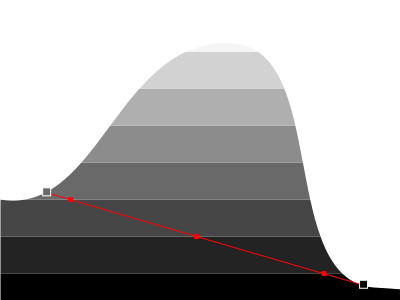
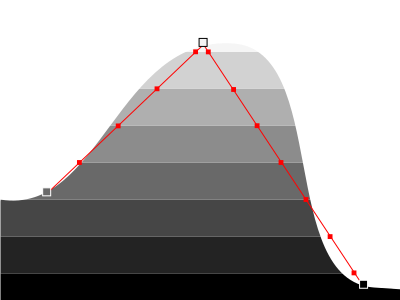
Also, although we know how many intersections we have, we have no idea where they are! Here we'll simply pretend the noise is linear and interpolate the positions.
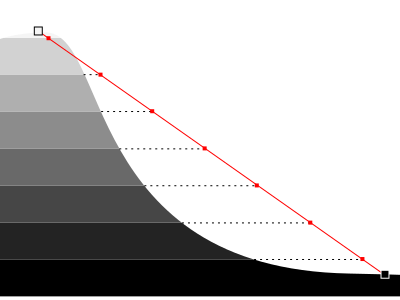
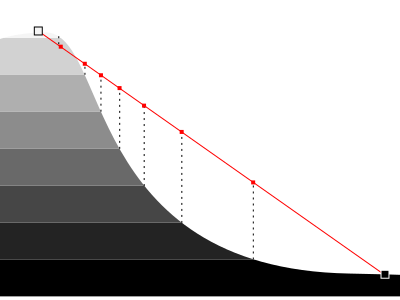
With these two approximations, we can miss some curves and misplace points. Still, the result is quite good (the marching squares algorithm does the same approximations) and if we want to improve the result we can use a finer grid.
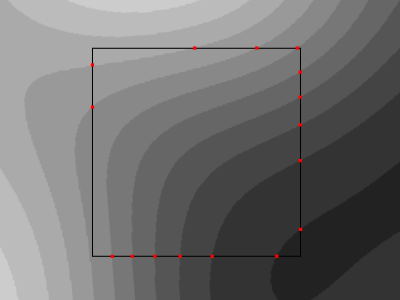
Step 2: connect the dots
Now we know the points that will compose our lines, we must connect them together.
If we just look at the points surrounding a cell we can't tell much about how we can connect them.
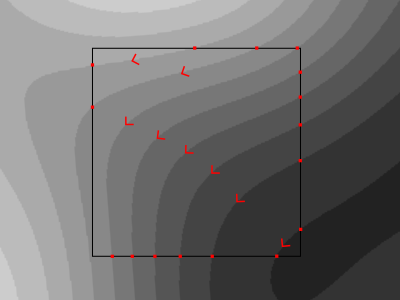
We can see isolines as paths between valleys and hills. If we always travel the isolines so that valleys are on the right and hills are on the left, then we can attribute consistent directions to them.
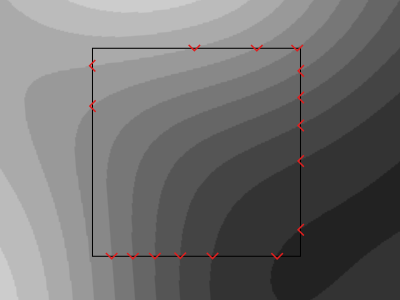
When looking at a cell we can now view some points as entry points and other at exit points. There is the same number of each and a segment must connect an entry point to an exit point.
Now we are very limited in how we can connect two points because as two lines can't cross each other some connection are just impossible
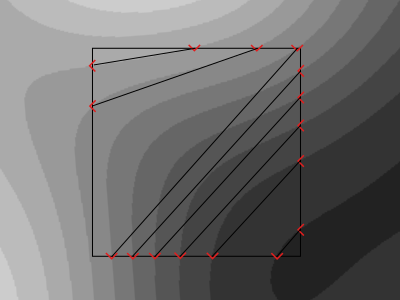
This last observation brings us to a simple algorithm:
We keep a pile of unconnected points (empty at first)
We go through each point in order around the cell and put them on top of a pile. If the two points on the top of the pile are of opposite direction (an entry point and an exit point) we connect them together and remove them from the pile.

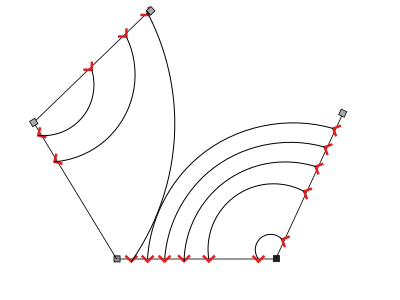

We can notice that for a given cell there are several possible configurations depending on where we start.


Some configurations are more accurate than others and it's possible to select the best one by looking more closely a the available sample or by taking extra samples.
We can also notice that an edge of the cell can only intersect with lines going in one same direction. So more edges means more alternance between entry and exit points and therefore more possible configurations. Three edges means a unique configuration and no ambiguity. However it's not a silverbullet, it only means we can't solve the ambiguity at this step and the result depends on how the grid is built.


As we go through the cells, we create, extend and merge parts of isolines. A linked list where the first and the last point reference each other is very efficient here. It allows us to detect when a path is closed and in the end to remove duplicates we might have collected.